
Avertissement: Cet article est une tentative d'explication des suites de Cauchy. J'y ai juste mis ce qui m'a aidé à comprendre ce concept, et j'espère juste que cela aidera d'autres personnes. Je ne suis pas un bon pédagogue, ni un bon matheux, et vous devriez prendre ce que vous lirez ici avec des pincettes. C'est dit !
Les profs de math sont vraiment trop nuls. On m'aurait dit : « Les suites de Cauchy, ce sont juste des suites convergentes avec une limite qui n'est pas dans notre espace », j'aurai compris tout d'suite.
Parce que le problème des suites convergentes, c'est que par définition, leur limite appartient à l'espace dans lequel on travaille. Mais si, par exemple, je considère la suite  dans
dans 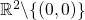 , on sait bien qu'elle tend vers
, on sait bien qu'elle tend vers 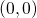 , mais on ne peut pas dire qu'elle soit convergente dans
, mais on ne peut pas dire qu'elle soit convergente dans 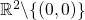 . Comme on trouvait ça un peu bête de pas pouvoir dire « mais siiiii, on sait bien qu'elle converge… on sait juste pas vers quoi ! », on a inventé la notion de suite de Cauchy. Cette définition nous permet de décrire toutes ces suites qui sont convergentes, mais vers quelque chose qui n'appartient pas à l'espace dans lequel on travaille.
. Comme on trouvait ça un peu bête de pas pouvoir dire « mais siiiii, on sait bien qu'elle converge… on sait juste pas vers quoi ! », on a inventé la notion de suite de Cauchy. Cette définition nous permet de décrire toutes ces suites qui sont convergentes, mais vers quelque chose qui n'appartient pas à l'espace dans lequel on travaille.

Alors oui, c'est un peu con de retirer le 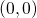 de
de  juste pour dégager la limite de
juste pour dégager la limite de  et avoir une suite de Cauchy non convergente… mais le truc c'est qu'il existe plein d'espaces dans lesquels on a des suites de Cauchy qui ne sont pas convergentes (pour de vrai), comme
et avoir une suite de Cauchy non convergente… mais le truc c'est qu'il existe plein d'espaces dans lesquels on a des suites de Cauchy qui ne sont pas convergentes (pour de vrai), comme  par exemple (où on trouve des suites qui tendent vers
par exemple (où on trouve des suites qui tendent vers 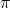 ). Ces espaces incomplets peuvent alors être complétés, en y ajoutant les « limites » de toutes ses suites de Cauchy, pour obtenir un espace où toutes les suites de Cauchy convergent, un espace complet.
). Ces espaces incomplets peuvent alors être complétés, en y ajoutant les « limites » de toutes ses suites de Cauchy, pour obtenir un espace où toutes les suites de Cauchy convergent, un espace complet.
Et tout ça c'est important, parce que le fait qu'un espace soit complet implique tout plein de propriétés plus utiles les unes que les autres, par exemple le critère de convergence absolue des séries, le théorème de Baire, ou le théorème du point fixe.
Generated by Org version 7.5 with Emacs version 23